GCN图卷积神经网络

学习了同济子豪兄对GCN卷积的讲解。

图卷积神经网络的基础知识

GCN本质上就是一种消息传递的节点计算图，他有几层就代表他通过几阶邻居来构建自己的嵌入，如下图，两层GCN网络表示它通过邻居和邻居的邻居来构建自己的嵌入。

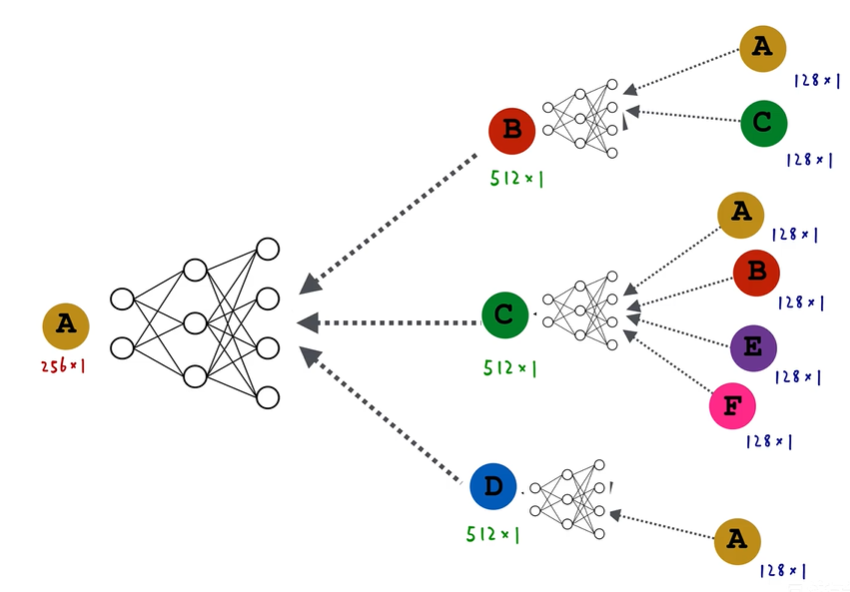
如下图，$x_v$表示输入节点的向量，它可以是一个one-hot编码（就是使用二进制表示某个节点）。每一层都是将邻居的信息加权平均后乘以一个权重并通过激活函数（这就是全连接神经网络）。

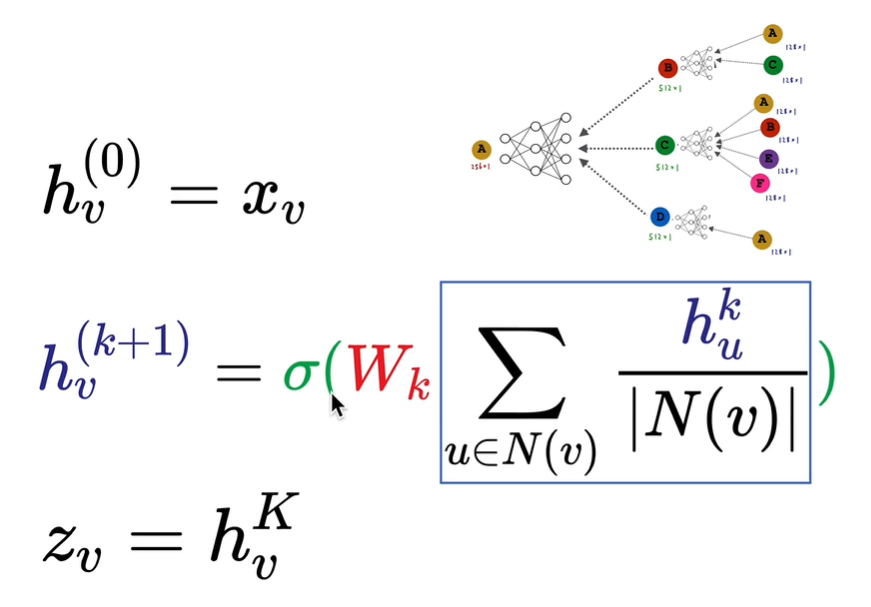
使用矩阵运算来进行化简，如下图，$H^{(k)}$表示每个节点的向量，第二行将累加求和的公式转换成矩阵乘法$AH^{(k)}$.左乘一个对角线矩阵的逆表示除以他的邻居总数。

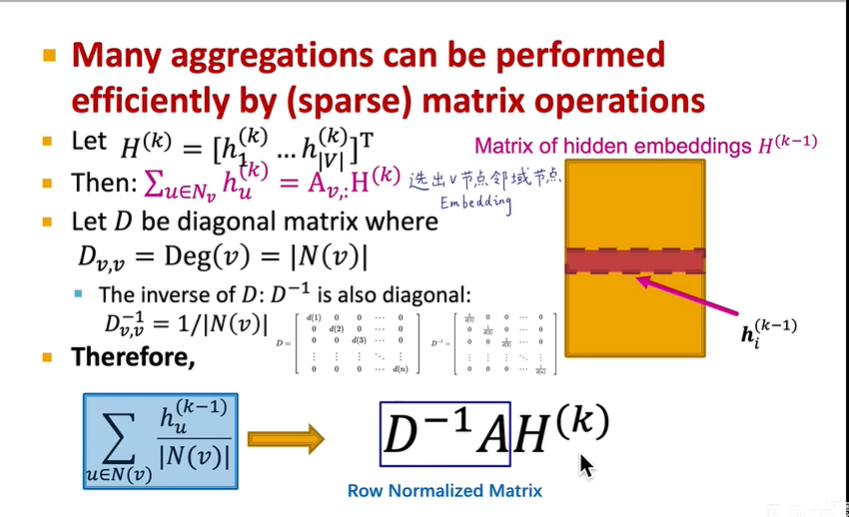
但是这样只考虑了自己的连接数，为了考虑对方的连接数应该再右乘一个对角线矩阵$D$，因此变为：

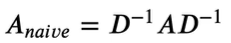
但此时有个问题，特征值会在（-1，1）之间，而我们希望他变为（-1，1]（不太明白作用，有人说是为了标准化），因此变为：

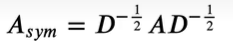
综上所述变为：

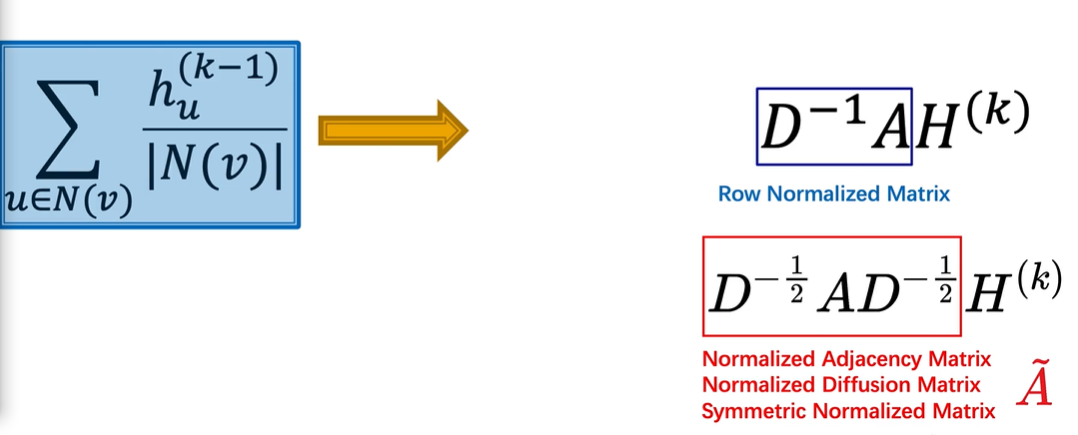
因此原文中的公式即得到，下面公式中的只有$W^{(l)}$是未知的：

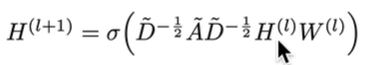
但是这样考虑还有一个问题就是没有考虑到自己对自己产生的影响，因此节点A的计算图应该考虑自己，他的做法为左下角的添加一个$I$单位矩阵。

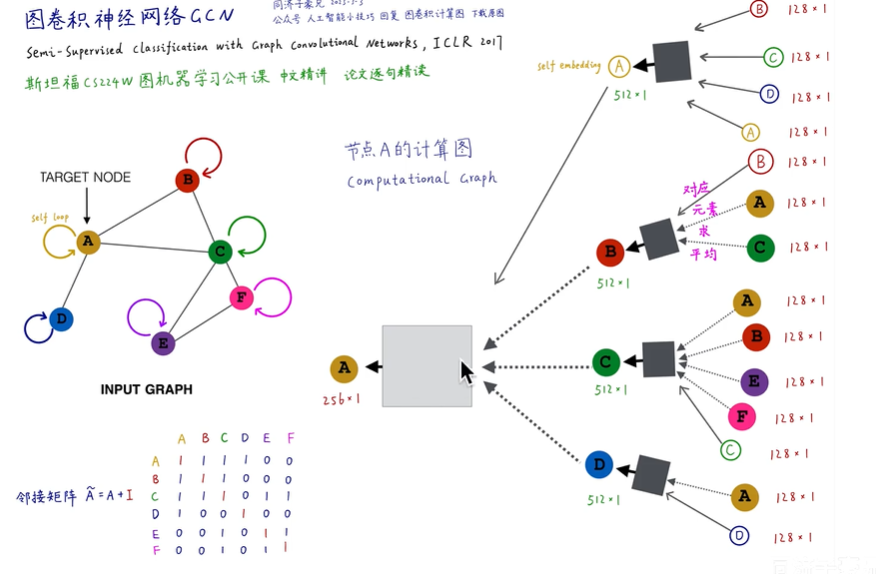
在图神经网络中的公式4.6就是同时考虑两个节点相互的影响（左右都乘$D^{-1/2}$）,并且考虑了自己的影响，4.7就是将自己的影响单独拆出来写。

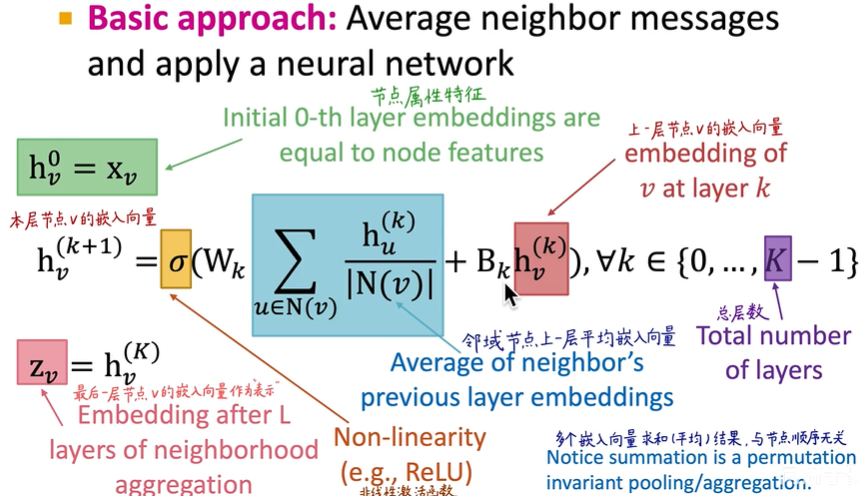
如果想邻域用一套权重，自己的self-embedding用一套权重，则公式如图所示，训练的只有$W$和$B$：

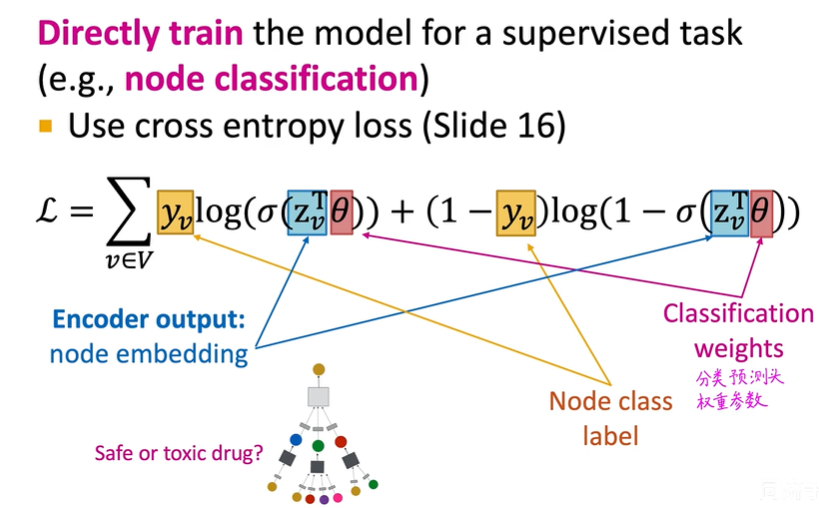
有监督训练

在训练的过程中使用交叉熵损失函数：

自监督训练

同时给两个节点已经他们的相似度来进行训练，相似度的定义可以通过：

随机游走
矩阵分解
图中的节点相似度

直推式学习与归纳式学习的区别

直推式学习（Transductive Learning）：预测的节点在训练时就见过，例如随机游走方法

归纳式学习（Inductive Learning）:用于预测的节点在训练时没见过（可以泛化新节点），例如GCN，GraphSAGE、GAT、GIN

将用户的特征加入到嵌入学习中，当遇到新用户时可以根据特征进行高效预测，这叫做“on the fly（冷启动、随来随用）”。

CNN和GCN的区别

CNN可以看作是一种特殊的GCN

图神经网络的表达能力

首先知道神经网络学习理论，只有层数够深可以拟合任意的输入和输出。

根据上面的计算图可以发现其实消息传递的GCN无法区分下面的节点1和节点2：

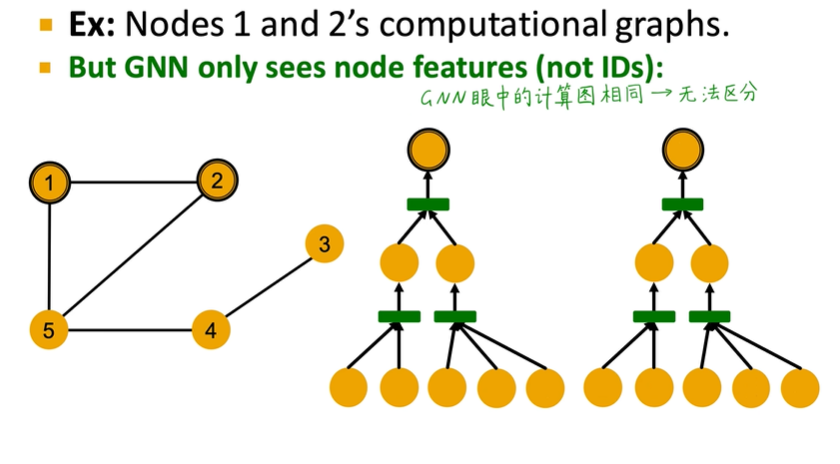
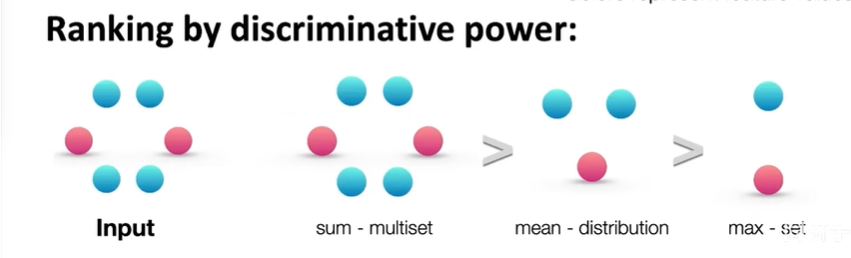
一个好的GCN虽然无法区分1、2但是必须能区分3、4、5。因此我们的聚合操作（每一层将邻居的嵌入聚合成一层的输出）应该是单射的。目前的聚合常见操作有相加，平均、最大，但效果都一般，因此延伸出一种表达能力最强的GCN网络GIN，GIN就是使用MLP去进行聚合操作，它是一种神经网络版的WL graph kernel（hash映射，算几轮就是捕捉了几个hop的邻居）。它还可以通过$\varepsilon$来控制有多关注邻域信息和自己的信息：

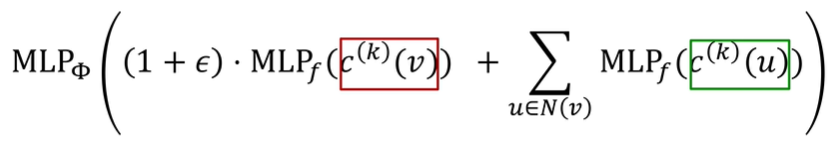
因此聚能方法表达能力的排序为：求和>平均>max

写在最后

如何区分1和2，可以使用节点属性信息。

引入随机属性
引入确定性距离属性
建立高阶图神经网络

GCN调参技巧

数据预处理：进行归一化
优化器：使用ADAM
激活函数：ReLu
节点嵌入维度：32、64、128
Debug 问题：模型训练过程0梯度、超参数、初始化权重、仔细观察损失函数。
测试集和验证集的损失函数是否出现了倒挂