• 自注意力机制

  学习了关于李宏毅的自注意力机制和Transformer相关内容

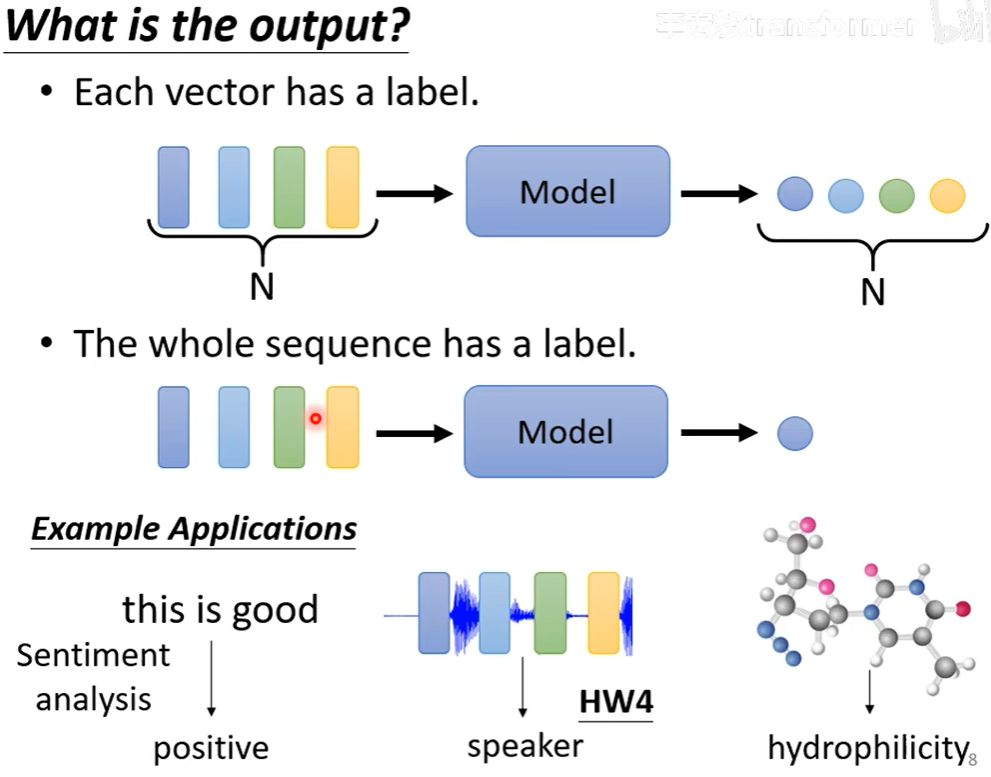
  机器学习有三种情况的输出，分别为：

  • 多个向量分别对应一个label
  • 多个向量对应一个label
  • 多个向量对应多个label

  

  自注意力机制

  Self-attention就是在使用的时候能够关注到整个句子的其他单词（向量）对于他的影响。

  

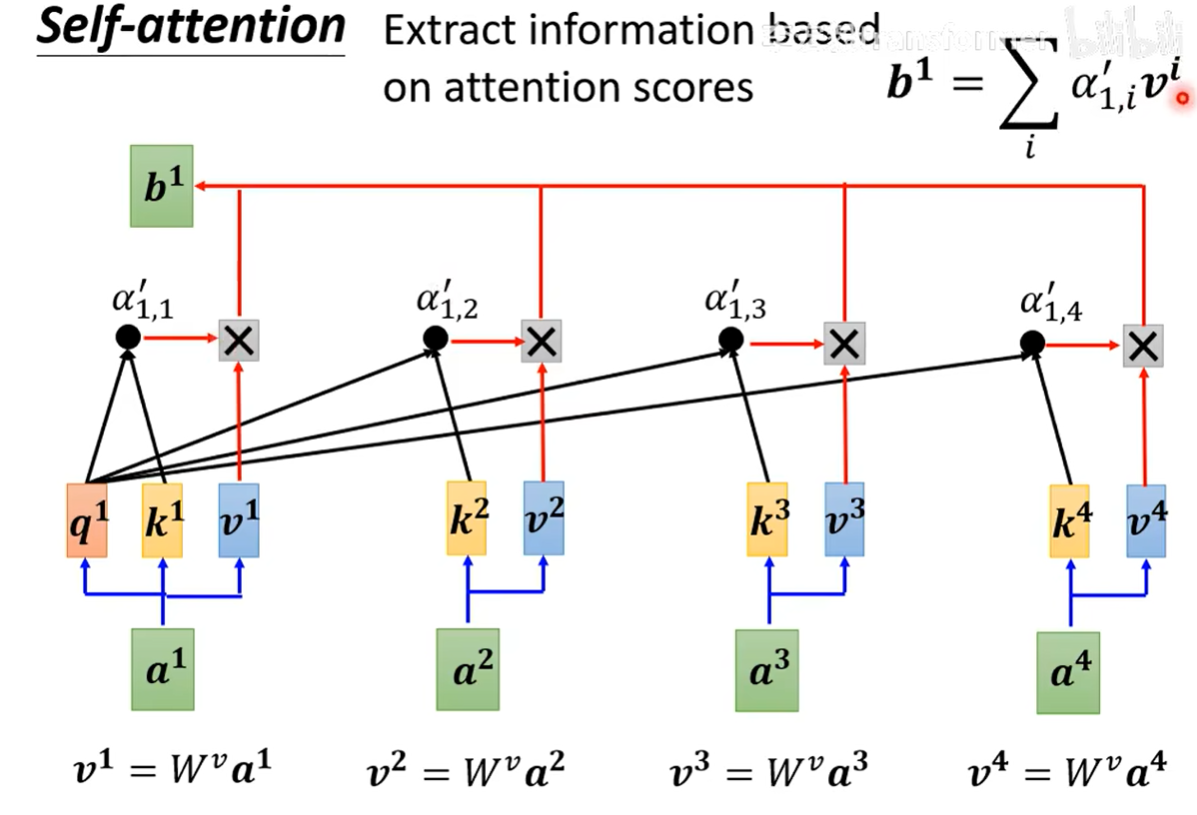
  对于上图来说，$a^1$就是一个单词的向量。在后续计算的时候可以发现他很像是数据库中的操作，因此自注意力中的$q^1,k^1,v^1$分别是query，key和value的缩写。当你想计算$a^1$通过自注意力算法得到的向量（考虑了其他向量的），首先你需要知道所有节点的$q,k,v$（通过矩阵乘法计算，非常快，后续会说一下），之后将$q^1$与其他所有节点（包括自己）的$k$相乘并通过softmax得到相关值$a’_{1,1}…$（softmax的合为1）。之后将这些值乘以所有节点的$v$即得到$a^1$通过注意力机制转换的向量。

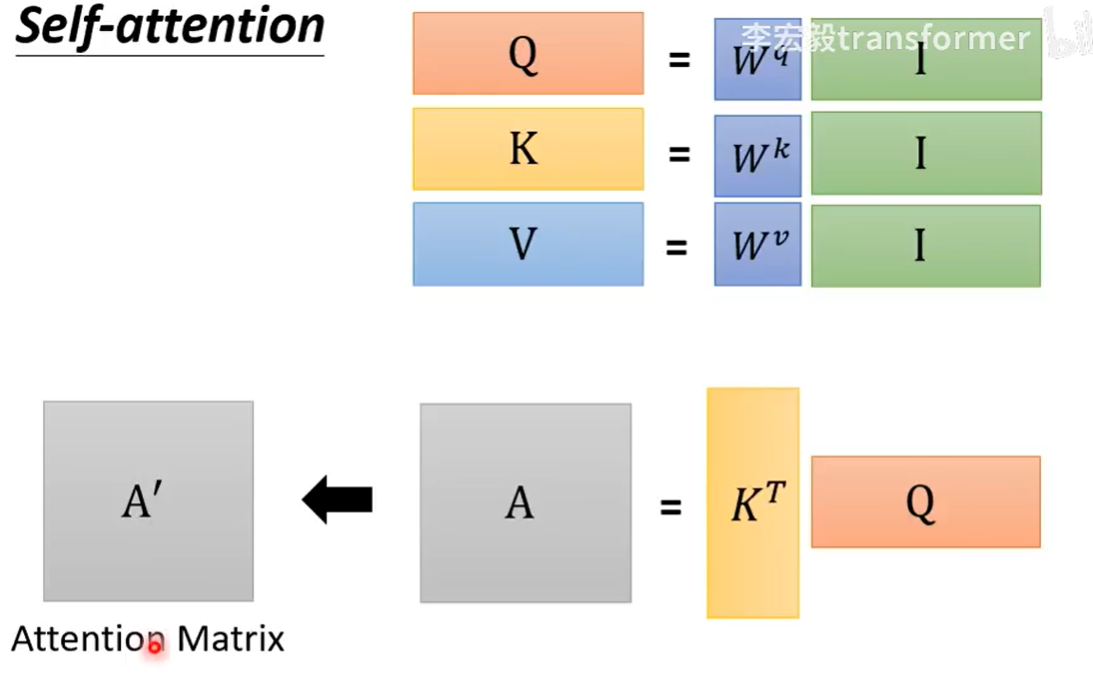
  下图是矩阵乘法计算QKV，可以看到其实计算出来非常的快，根据矩阵运算的本质就是将I分别放到$W^q,W^k,W^v$的空间。之后再通过矩阵QK来计算相似度。

  

  多头注意力机制（Multi-head Self-attention）

  

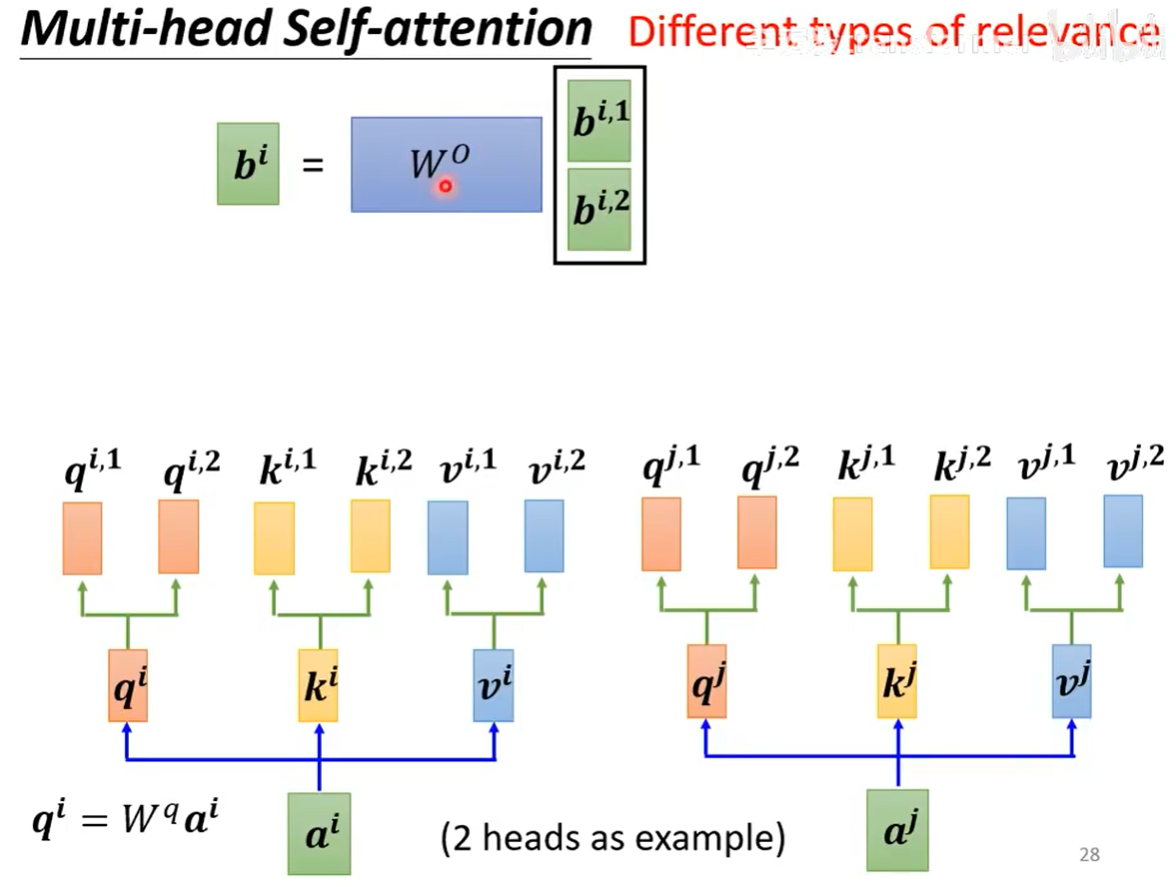
  与普通的注意力机制相似，只是做了两次attention后通过一个权重矩阵接起来（多头的好处是可以避免初始值造成的影响）。

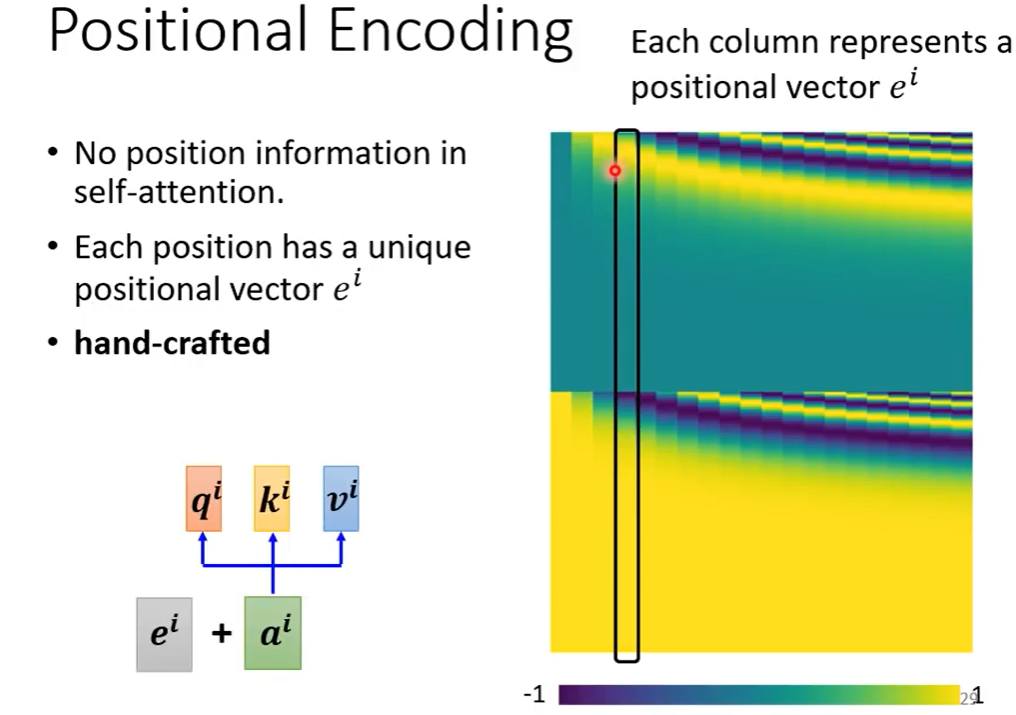
  位置编码（Positional Encoding）

  但是目前的方法没有位置信息，因此我们需要加入一点位置区分，通常是人为设置，可以搜一下目前常用的位置编码方法。

  

  自注意力与其他卷积方法的对比

  CNN就是self-attention的特例，self-attention的范围是人决定的，而CNN是根据人为的感受野大小决定

  RNN不能并行处理，自注意力可以平行处理。并且如果要感知上下文的话需要使用双向RNN。